Optimizer
 Previous  Next
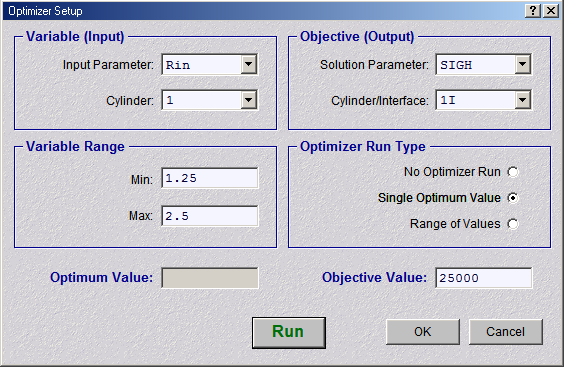
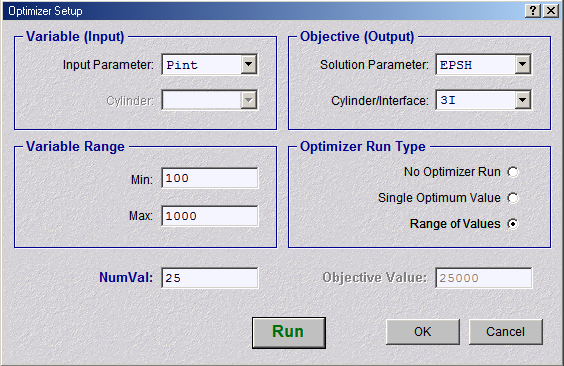
The Concyl optimizer can be used for two types of runs:  a "single optimum value" run (hereafter referred to as a "single-value" run) or a "range of values" run (hereafter referred to as a "range" run).   The run type and all other optimizer input are specified on the optimizer dialog shown in Figure 9.  Figure 9a shows the dialog for the single-value run, and Figure 9b shows the dialog for the range run. 

Model Parameter To Optimize Cylinder To Be Optimized Lower Limit For Search Window Upper Limit For Search Window Optimum Value (Output) Objective Parameter Objective Cylinder and Interface Select Run Type Objective Value (Target) Press To Run Optimizer
Figure 9a.  Optimizer Setup Dialog, Single-Value Run



Model Parameter To Optimize Cylinder To Be Optimized Input Variable Lower Limit Input Variable Upper Limit Number of Runs Objective Parameter Objective Cylinder and Interface Select Run Type Press To Run Optimizer
Figure 9b.  Optimizer Setup Dialog, Range Run

A single-value optimization run computes a single value for a model input quantity (the variable) that yields a specified value for a specified solution output quantity (the objective).  A range run generates a range of solution values based on a range of input values for a specified model quantity.  The available input and output parameters are listed below. 

Available Model Input (Variable) Parameters

1. Rin = cylinder inner radius
2. Rout = cylinder outer radius
3. E = cylinder tensile modulus
4. nu = cylinder Poisson ratio
5. alpha = cylinder coefficient of thermal expansion
6. To = cylinder stress free temperature
7. Temp = applied uniform temperature to all cylinders
8. Pint = applied inner pressure
9. Pout = applied outer pressure
10. EPSZ = applied axial strain to all cylinders

Available Solution Output (Objective) Parameters

1. SIGR = radial stress
2. SIGH = hoop stress
3. SIGZ = axial stress
4. TAUMAX = max shear stress
5. EPSR = radial strain
6. EPSH = hoop strain
7. EPSZ = axial strain
8. GAMMAX = max shear strain
9. DISPR = radial displacement

Note that input parameters 1 through 6 are related to individual cylinders in the system, while input parameters 7 through 10 relate to the entire system.  Therefore, input parameters 1 through 6 require that a relevant cylinder be specified, while parameters 7 through 10 do not require a cylinder to be specified. 
All of the output parameters require that the cylinder and cylinder interface be specified.  The interface is either the inner or outer surface of the cylinder which is denoted by an I or O respectively.  The interface is needed because the solution quantities such as stress and mechanical strain are highly dependent on the material properties for each cylinder.  These material-dependent solution quantities will, in general, be discontinuous across the interfaces between cylinders with different materials.  Of course, other solution quantities, such as total strain and displacement, are always continuous across the cylinder interfaces.
Single Value Optimization
The single-value optimization run will search between the specified lower and upper bounds until it finds the optimum input parameter value that produces the desired solution quantity value.  If this optimum input value is found, then it is displayed in the dialog shown in Figure 9a.  If no optimum value could be found, then an appropriate error message is displayed.  The user can then change the objective value or change the input variable range and attempt another solution.  The search is done using a simple bisection search algorithm.  This requires good choices for the lower and upper range limits.  Otherwise, no optimum solution can be found.  It is also very possible that the desired optimum value for the output parameter cannot be achieved for any range of input parameter values.  Therefore, it is recommended that before a single-value optimization is attempted, the user should first do a range-value run and plot the results to see visually how the input and output values are related. 
Figure 9a above shows the optimizer GUI settings that compute the required bore radius needed to achieve a bore hoop stress (SIGH) of 25000.  The optimizer will search for an optimum inner radius for cylinder 1 between the specified lower and upper limits of 1.55 and 2.5 respectively. The "Concyl-Opt.txt" output file will have the cylinder 1 inner radius as column 1 and the hoop stress at the cylinder 1 inner surface for column 2. 
Range Run
The range run does no searching.  Instead, it simply does a series of runs while varying the specified input parameter from the lower limit to the upper limit.  The number of equally spaced runs is specified on the dialog shown in Figure 9b.  This is useful for plotting to visualize how the output parameter varies with the input parameter.  For example, the user can readily determine how the bore hoop stress varies with applied the temperature or pressure. 
Figure 9b above shows an example of a range run that will generate results for 25 runs while varying the internal pressure from 100 to 1000.  The output file will have the applied pressures listed  in column 1 and corresponding the inner surface hoop strains for cylinder 3 will be listed in column 2.
Both types of optimization runs produce a tab-delimited output file named "Concyl-opt.txt".  This file has the list of input parameter values for the first column.  The second column has the corresponding requested solution parameter values.  The remaining columns have the rest of the solution parameter values.  A header line is included to label all of the columns.   This file can be readily imported into a plotting program such as Microsoft Excel for subsequent visualization.