Test 1

Test Problem 1 (Rotation About Z Axis)

Previous Top Next

Verification Test 1 is the most simple type of 3D rotational transformation with a single rotation about the Z axis. This test has two cases: Case 1 computes the components of a fixed vector in a rotated reference frame. Case 2 computes the components of a rotated vector given the unrotated vector components in the same reference frame. Exact solutions for this problem are done manually and then compared against the QuatView results. The manual solutions are done using two methods: the rotation matrix and the rotation quaternion. The QuatView results agree precisely with both manual solutions which verifies that the QuatView vector rotation calculations are correct.

Given:

1. Two 3D right-handed Cartesian reference frames, Frame A and Frame B, with Frame B oriented at a counterclockwise angle of 30° about the Z axis of Frame A (see Figure C1-1).

2. A fixed 3D vector with coordinates given in Frame A as (0.6, 0.8, 0.0).

Find:

1. The vector coordinates with respect to Frame B.

2. The vector coordinates with respect to Frame A if the vector is not fixed and instead rotates counterclockwise with an angle of 30°.

Solution:

Case 1:

Case 1 considers a fixed 3D vector that is defined with respect to Frame A as

V^A = (0.6, 0.8, 0.0).

Another frame, designated as Frame B, is rotated by a counterclockwise angle, q = 30° about the Z axis with respect to Frame A. The objective of this case is to determine the components of the vector V with respect to Frame B.

The input vector, V, has a magnitude of unity and an angle b of 53.13° with respect to the X_A axis. Figure C1 shows V, Frame A, and Frame B, along with the angles q and b.

The solution to this problem is computed manually using two methods: the rotation matrix and the rotation quaternion. The results from these two methods are then compared against the output from QuatView.

A) DCM Solution:

The basic formula for doing a rotational transformation on a vector is

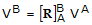(C1-1)

where V^A is the vector with respect to Frame A, V^B is the vector with respect to Frame B, and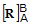

is the DCM that defines the orientation of Frame B with respect to Frame A. Each element of the DCM is given by cos(a_ij), where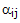

is the angle between the i'th axis of Frame B and the j'th axis of Frame A. The matrix row number is i and the column number is j. So, looking at Figure C1-1, the first element of the first row is the cosine of the angle between axes X_B and X_A which gives cos(q). Similarly the second element of the first row is the cosine of the angle between axes X_B and Y_A which gives cos(90-q) which is equal to sin(q). Finally, the third element of the first row is the cosine of the angle between axes X_B and Y_A which gives cos(90)=0. Using this approach for the remaining rows, all of the elements of the DCM can be computed as

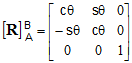(C1-2)

Eqn. C1-2 is the general DCM for expressing the coordinates of any vector in a rotated frame where the rotation is a counterclockwise angle, q, about the Z axis of the original (unrotated) frame. Note that this equation is only valid if both frames have right-handed coordinate systems.

Figure C1-1. Verification Test 1, Case 1 - V Is Fixed To Frame A

Plugging the given value for q=30° into Eqn. C1-2 gives the DCM as

Using this DCM in Eqn. C1-1 and performing the matrix multiplication then gives the following values for the vector components in Frame B:

Therefore, the requested vector components with respect to Frame B are

V^B = (0.9196, 0.3928, 0.0000) <-------ANSWER

B) Quaternion Solution:

The same solution can be computed with quaternions using the quaternion rotation formula

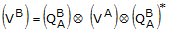(C1-3)

where (V^A) and (V^B) are pure quaternions containing the vector components V^Aand V^B,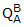

is the rotation quaternion defining the orientation of Frame B with respect to Frame A,

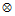is the quaternion multiplication operator, and * is the quaternion conjugate operator.

The rotation quaternion that represents the orientation of Frame B with respect to Frame A is given by the standard formula

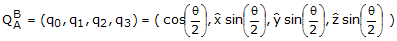(C1-4)

where q is the counterclockwise angle about the rotation axis from Frame A to Frame B and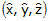

are the components of the rotation axis. Since the rotation axis for this problem is the Z axis of Frame A, the rotation axis vector is simply (0,0,1). This means that the quaternion components q₁ and q₂ are zero, and component q₃ is given by

q₃ = sin(q/2) = sin(15) = 0.2588

The scalar component, q₀, is then

q₀ = cos(q/2) = cos(15) = 0.9659

The quaternion that defines the orientation of Frame B with respect to Frame A is then

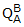= (0.9659, 0.0, 0.0, 0.2588)

The pure quaternion for (V^A) is simply

(V^A) = (0.00, 0.60, 0.80, 0.00)

Plugging these values for (V^A) and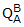

into Eqn. C1-3 gives

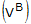= (0.9659, 0.0, 0.0, 0.2588)

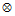(0.00, 0.60, 0.80, 0.00)

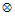(0.9659, 0.0, 0.0, -0.2588)

Performing the two quaternion multiplications in accordance with Eqn. 2 involves a fairly lengthy amount of algebra, all of which will not be repeated here. The end result of the quaternion multiplications is

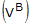= (0.00, 0.9196, 0.3928, 0.00)

Separating out the vector from the pure quaternion then gives the following final answer for the vector components in Frame B:

V^B = (0.9196, 0.3928, 0.0000) <-------ANSWER

This answer agrees precisely with the answer from the DCM solution, which is to be expected.

C) QuatView Solution:

Figure C1-2 shows the QuatView screen shot for this verification problem. The orientation of Frame B with respect to Frame A is defined by the three Euler angles entered as (0.0, 0.0, 30.0). The input vector, which is defined in Frame A as (0.6, 0.8, 0.0), must also be entered.

Figure C1-2. QuatView Results For Case 1 (Fixed Vector in Rotated Frame)

Vector plotting is also turned on using the Options dialog. The vector initial reference frame must also be set to the default setting of "Frame B (Rotating)" using the Options dialog.

Once the Frame B orientation and vector components are entered, then QuatView automatically displays the complete solution which includes the Frame B orientation quaternion and the fixed vector components in Frame B.

Taking the results directly from Figure C1-2 gives

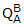= (0.9659, 0.0, 0.0, 0.2588) <-------- Quaternion For Frame B

V^B = (0.9196, 0.3928, 0.0000) <-------ANSWER

These answers agree precisely with the manual solutions given above. This validates the QuatView vector rotation calculations.

Case 2:

Case 2 considers the same input vector as Case 1, except that for Case 2 this vector is rotated counterclockwise by an angle of q = 30° about the Z axis instead of being fixed. The objective of this case is to determine the components of the rotated vector with respect to Frame A.

Figure C1-3 shows the vector in its unrotated (V_A) and rotated (V_B) orientations with respect to Frame A. The angles q and b are also shown, where b = 53.13° is the initial vector orientation angle prior to the rotation. The final orientation angle after the rotation is then (q+b).

Figure C1-3. Verification Test 1, Case 3 - V Rotates With Frame B

The solution to this problem is computed manually using two methods: the DCM and the rotation quaternion. The results from these methods are then compared against the output from QuatView.

It turns out that Case 1 and Case 2 are closely related, with solution procedures that are very similar. In fact, the DCM solution for Case 2 is the same as Case 1 with the only difference being that the transpose of the Case 1 DCM is used for Case 2. Likewise, the only difference with the quaternion solution is that the rotation quaternion transpose for Case 2 appears on the LHS of equation C1-3 instead of on the RHS.

A) DCM Solution:

The basic formula for rotating a vector is

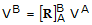(C1-5)

where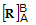

is the DCM that defines the vector rotation from A to B. The simplest way to derive this DCM is to relate the final and initial vector components in accordance with Figure C1-3. As this figure shows, with a vector magnitude of unity the initial vector components (x_A,y_A) are given by

x_A = cos(b)

y_A = sin(b) (C1-6)

Similarly, the final vector components are given by

x_B = cos(q+b)

y_B = sin(q+b) (C1-7)

Using the trigonometric formulas for the sine and cosine of the sum of two angles then yields

x_B = cos(q+b) = cos(q)cos(b) - sin(q)sin(b)

y_B = sin(q+b) = sin(q)cos(b) + cos(q)sin(b) (C1-8)

Substituting Eqns. C1-6 into C1-8 then gives

x_B = x_Acos(q) - y_Asin(q)

y_B = x_Asin(q) + y_Acos(q) (C1-9)

Putting Eqns. C1-9 into matrix format per Eqn. C1-5 then gives the DCM as

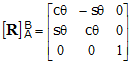(C1-10)

Plugging q=30° into Eqn. C1-10 then gives the following DCM:

Note that this DCM is simply the transpose of the DCM used for Case 1. This means that expressing a fixed vector in a rotated reference frame is the transpose of rotating the vector with respect to a fixed frame.

Performing the matrix multiplications in Eqn. C1-5 gives the rotated vector components as

The requested vector components with respect to Frame B are then

V^B = (0.1196, 0.9928, 0.0000) <-------ANSWER

B) Quaternion Solution:

The quaternion transformation formula for a rotating vector in a fixed coordinate system is given by

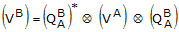(C1-11)

where (V^A) and (V^B) are pure quaternions containing the vector components V^Aand V^B,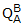

is the rotation quaternion defining the orientation of Frame B with respect to Frame A,

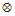is the quaternion multiplication operator, and * is the quaternion conjugate operator. Note that this formula is similar to Eqn. C1-3 from Case 1 with the only difference being that the rotation quaternion transpose is on the LHS instead of the RHS.

Using Eqn. C1-4, the rotation quaternion for a counterclockwise rotation from A to B with q = 30° is computed as

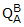= (0.9659, 0.0, 0.0, 0.2588)

The pure quaternion for the input vector is the same as Case 1 which is given by

(V^A) = (0.00, 0.60, 0.80, 0.00)

Plugging these values for (V^A) and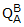

into Eqn. C1-11 gives

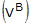= (0.9659, 0.0, 0.0, -0.2588)

(0.00, 0.60, 0.80, 0.00)

(0.9659, 0.0, 0.0, 0.2588)

Performing the two quaternion multiplications in accordance with Eqn. 2 gives

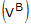= (0.00, 0.1196, 0.9928, 0.00)

Separating out the vector from the pure quaternion then gives the following final answer for the vector components in Frame B:

V^B = (0.1196, 0.9928, 0.0000) <-------ANSWER

This answer agrees precisely with the answer from the DCM solution, which is to be expected.

C) QuatView Solution:

Figure C1-4 shows the QuatView results for Case 2. The orientation of Frame B with respect to Frame A is defined by the three Euler angles entered as (0.0, 0.0, 30.0). The vector is entered in Frame A as (0.6, 0.8, 0.0). The vector initial reference frame must be set to "Frame A (Fixed)" using the Options dialog. Vector plotting is also turned on using the Options dialog.

Figure C1-4. QuatView Results For Case 2 (Rotated Vector in Fixed Frame)

Once the rotation angles and vector components are entered, then QuatView automatically displays the complete solution which includes the Frame B rotation quaternion and the rotated vector components with respect to Frame A.

Taking the results directly from Figure C1-4 gives

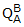= (0.9659, 0.0, 0.0, 0.2588) <-------- Quaternion For Rotated Vector

V^B = (0.1196, 0.9928, 0.0000) <-------ANSWER

These results agree precisely with the manual solutions given above using the DCM and quaternion methods. This validates the QuatView vector rotation calculations.