Quaternion Background
 Previous Top Next
What is a quaternion?
A quaternion is a mathematical abstraction just like a real number, complex number, tensor, or manifold.  A quaternion is basically a type of complex number that consists of four values, one of which is real, while the other three are imaginary.  As such, quaternions are referred to as hypercomplex numbers.  So, just like a complex number consists of two parts (real and imaginary), the hypercomplex number consists of four parts (1 real and 3 imaginary).  The mathematical properties of hypercomplex numbers are such that quaternions, when normalized, are ideally suited for representing the orientation of an object in 3D space and for transforming the orientation coordinates between any two 3D reference frames.  Another name for the normalized quaternion is the versor. 
Several textbooks and internet references are available that provide detailed descriptions of quaternions, including mathematically rigorous derivations of all the relevant quaternion rules and formulas.  A short list of quaternion references is given here.   
There are two common conventions for representing a quaternion: one has the real component first and the other has the real component last.  QuatView uses the former convention with the following notation for the quaternion, q.
      graphic
where,
      graphic
A quaternion can be normalized just like a four dimensional vector by dividing each of the four components by the Euclidean norm.  The Euclidean norm is defined as the square root of the sum of the squares of the four quaternion components. 
Physical Interpretation
The normalized quaternion can be interpreted physically as an angle combined with a 3D axis about which a single rotation defines the final orientation of a frame relative to some initial reference frame.  According to Euler's rotation theorem, the orientation of any object in 3D space can be defined by a single rotation about a single axis.  Figure 20 shows a rotation axis, 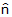graphic, and a rotation angle, q, about this axis. 
graphic
Figure 20.  Quaternion as rotation axis and angle

A quaternion can then be defined that represents a rotation from Frame A to Frame B.  That is, a quaternion can be defined that represents the orientation of Frame B with respect to Frame A.  The components of this quaternion are related to the rotation axis and angle in Figure 20 according to the following formulas:
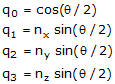         graphic                                                                  (1)
where,
         graphic
         graphic
The scalar component of the quaternion gives the rotation angle, and the three imaginary components, when normalized, give the direction of the rotation axis. 
The rotation angle is then readily computed from the arc cosine of the quaternion scalar component as
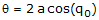      graphic                                                                                         (2)
The quaternion has its own special set of mathematical operations so that it can be used very effectively for simulating and predicting rotational motion.  
Quaternion Product
The quaternion product is perhaps the most important quaternion operation since it is used extensively in vector transformation and rotational kinematics.  It is also used to compute the quaternion derivative.  Multiplying two quaternions together is a fairly complex process compared to vector multiplication.  Separating each quaternion into scalar and vector components, the formula for multiplying two quaternions can be expressed as
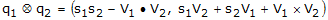      graphic                          (3)
where,
      graphic
      graphic
    si = scalar (real) component for quaternion i
     Vi = vector (imaginary) components for quaternion i
     graphic = quaternion product
     graphic = vector dot product
     graphic = vector cross product

This formula shows that the quaternion product requires five individual products including a vector dot product and a vector cross product. 
Quaternion Conjugate
The quaternion conjugate is similar to the conjugate for standard complex numbers except that the quaternion has three imaginary numbers instead of only one.  So the quaternion conjugate is computed by reversing the sign of the three imaginary components.
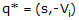      graphic                                                                           (4)
where,
     q* = quaternion conjugate
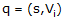      graphic= quaternion
     s = real component
     Vi = imaginary components (i = 1,2,3)
Quaternion Magnitude
The quaternion magnitude is a scalar value that is equal to the four dimensional Euclidean norm which is simply the square root of the sum of the squares of the four components. 
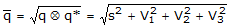      graphic                                             (5)
where,
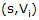
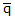     q = quaternion, graphic
     graphic= quaternion magnitude
    q* = quaternion conjugate
     s = real component
     Vi = imaginary components (i = 1,2,3)
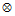     graphic = quaternion product
Quaternion Inverse
The quaternion inverse is computed by dividing its conjugate by its magnitude squared as shown in the following formula:
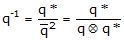      graphic                                                                  (6)
where,
     q = quaternion
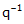     graphic= quaternion inverse
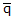     graphic= quaternion magnitude
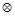     graphic = quaternion product
Normalized Quaternion
A quaternion must be normalized to represent a valid 3D orientation or to compute valid vector rotations.  Normalized quaternions, or versors, have the special property that their conjugate is equal to their inverse.  When quaternions are used in numerical simulations to represent orientations, the quaternion must be renormalized at frequent intervals to account for the accumulation of numerical round off error.  A normalized quaternion (or unit quaternion) is computed by simply dividing the quaternion by its magnitude.
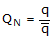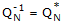      graphic,    graphic                                                               (7)
where,
     QN = normalized quaternion
     q = unnormalized quaternion
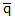     graphic= quaternion magnitude
Pure Quaternion
A pure quaternion is defined as a quaternion with a zero for the scalar value (q0=0). A standard 3D vector can be readily stored in a pure quaternion.  Pure quaternions can then be used to rotate vectors or transform the vector coordinates between different rotated reference frames. 
Vector Transformation
The components a vector can be transformed between any two different reference frame orientations using the following formula:
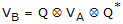      graphic                                                                   (8)
where,
     VA = vector (pure quaternion) in Frame A coordinates
     VB = vector (pure quaternion) in Frame B coordinates
     Q = normalized quaternion for orientation of Frame B relative to Frame A.
     Q* = conjugate (or inverse) of Q
     graphic = quaternion product
Quaternion Time Derivative
If the quaternion, q, represents the orientation of a rotating Frame B relative to some other reference Frame A, then the quaternion rate or time derivative of this quaternion can be expressed in terms of the corresponding angular velocity vector, w, that defines the rate at which Frame B rotates relative to Frame A.  This angular velocity vector can be expressed in terms of Frame A or Frame B coordinates as wA or wB respectively.  The formula for the quaternion derivative is given by
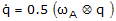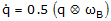      graphic   or    graphic                                    (9)
where,
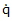     graphic = quaternion rate of Frame B relative to Frame A
     q = quaternion for Frame B orientation relative to Frame A
     wA = angular velocity of Frame B in Frame A coordinates
     wB = angular velocity of Frame B in Frame B coordinates
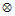     graphic = quaternion product